Come il pensiero statistico aiuta a prendere decisioni corrette in un mondo incerto
TEORIE > METODI > INTELLIGENZA UMANA
Scopo di questa pagina
Di solito si intende per statistica solo la cosiddetta "statistica descrittiva", che prende atto di ciò che accade e lo trasforma in numeri sulla base di rilevazioni effettuate sulla "popolazione" oggetto dell'indagine (ad esempio le statistiche ISTAT sull'intera popolazione). Ma esiste un altro tipo di statistica, detta "statistica inferenziale", che prende un sottoinsieme limitato di misure (un "campione") e fa delle inferenze "rischiose" generalizzando all'intera popolazione le conclusioni probabilistiche svolte sul campione. Lo psicologo Gerd Gigerenzer sostiene che oggi, a scuola, si insegna ancora la "matematica della certezza" (geometria, trigonometria, ecc) ma non la "matematica dell'incertezza", cioè la "statistica inferenziale". La tradizionale visione "oggettiva" della probabilità subisce una profonda modificazione a metà del 1700, con il Teorema del pastore presbiteriano Thomas Bayes, il quale inaugura una visione "soggettiva" della probabilità che la vede dipendere dall'esperienza accumulata dallo sperimentatore e, quindi, dal variare della sua conoscenza o ignoranza dell'evento. Il Teorema di Bayes spiega come cambia la probabilità di un evento se (o dato che) sono accaduti altri eventi, quindi il Teorema di Bayes mostra come fare valutazioni di probabilità e modificarle successivamente in presenza di nuovi dati.
There is uncertainty about the future.
Let's enjoy it, because when it becomes certainty it will be hard.
Let's enjoy it, because when it becomes certainty it will be hard.
Punto chiave di questa pagina
IMPARARE A RISCHIARE: Saper leggere e scrivere non è più sufficiente in una società tecnologica, sempre più complessa, nella quale i rischi si moltiplicano. Nè, tantomeno, è sufficiente saper far di conto in modo tradizionale, almeno questo è il parere dello psicologo Gerd Gigerenzer il quale sostiene che oggi, a scuola, si insegna ancora la "matematica della certezza" (geometria, trigonometria, ecc) ma non la "matematica dell'incertezza", cioè la "statistica inferenziale". Per vivere nel mondo attuale occorrerebbe, secondo Gigerenzer, che la "buona scuola" insegnasse due competenze: una conoscenza di base della psicologia intuitiva e la capacità di capire le statistiche. Scrive Gigerenzer nel libro "Imparare a rischiare" (pp. 289-291): "Ai nostri figli vengono insegnati l'algebra, la geometria, i fondamenti del calcolo infinitesimale e il calcolo infinitesimale stesso. In altre parole insegniamo loro la matematica della certezza e non quella dell'incertezza, ovvero il pensiero statistico. Quanti di noi hanno bisogno, sul lavoro o a casa, di risolvere equazioni quadratiche, calcolare l'intersezione di un cubo con un piano o riflettere sui numeri irrazionali? E' stato detto che esercitarsi in discipline astratte come l'algebra e la geometria migliora la qualità del pensiero e la capacità di risolvere problemi. Se fosse vero, non avremmo tutti questi dottori che non capiscono le statistiche sanitarie o tutti questi avvocati che non capiscono la prova del DNA. [...] Bisogna insegnare prima quello che è importante per la vita reale, e solo dopo quello che è importante in matematica. L'orientamento alla soluzione di problemi della vita reale anzichè a una matematica astratta rende essenziali una presentazione trasparente, strumenti pratici e regole del pollice intelligenti - ma per realizzare cose così nuove bisogna insegnare agli insegnanti. Bisogna insegnare prima quello che è importante per la vita reale, e solo dopo quello che è importante in matematica. L'orientamento alla soluzione di problemi della vita reale anzichè a una matematica astratta rende essenziali una presentazione trasparente, strumenti pratici e regole del pollice intelligenti - ma per realizzare cose così nuove bisogna insegnare agli insegnanti."
Punti di riflessione
Il problema [degli errori decisionali] non è semplicemente l'ottusità degli esseri umani, ma il fenomeno di una "società non alfabetizzata al rischio". (Gerd Gigerenzer p.4)
-
Nella misura in cui le leggi della matematica si riferiscono alla realtà, esse non sono certe; e nella misura in cui sono certe, non si riferiscono alla realtà. (Albert Einstein)
-
Parecchi studi hanno dimostrato che i decisori umani sono meno affidabili di una formula predittiva anche quando viene fornito loro il punteggio suggerito dalla formula! Ritengono di poter scartare la formula perchè dispongono di ulteriori informazioni sul caso, ma quasi sempre si sbagliano. (Daniel Kahneman p.247)
-
Risolvere un problema significa solo rappresentarlo in modo da rendere trasparente la soluzione. (Herbert A. Simon)
-
-
Gli strumenti della statistica tradizionale misurano solo una parte dei fenomeni. Danno una fotografia che rappresenta elementi visibili, espliciti, dai contorni definiti. Quello che non catturano è l'emozione. (Guido Tripaldi)
_
La differenza chiave tra statistica e causalità è che la prima prevede il futuro da osservazioni passive, mentre la seconda prevede i risultati di azioni, interventi o politiche. Prevedere i risultati di un'elezione sulla base dei dati dell'indagine è un compito statistico, ben studiato e ben inserito nella vecchia scienza. Ma prevedere i risultati dell'innalzamento del salario minimo è un compito causale, poiché comporta un intervento attivo, quindi non può essere realizzato utilizzando metodi tradizionali. (Judea Pearl)
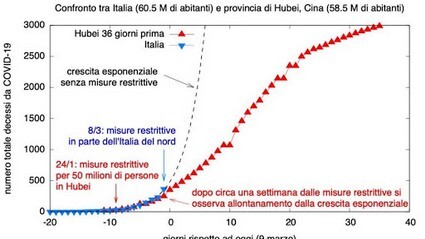
Come la statistica aiuta ad agire contro l'epidemia di Covid-19
La statistica è utile di fronte a un'epidemia, come dice in un'intervista l'epidemiologo Alessandro Vespignani (vedi bibliografia 2020):
Vespignani spiega come si può fare in modo semplice, quello che lui chiama le tre T: “testing, tracing and treating”. Testare: «Tamponi e test» afferma: «Purché omologati. Serve un esercito. Serve una determinazione ossessiva e spietata. Io in Italia oggi questo esercito non lo vedo». Tracciare: «Che poi significa poter “Isolare”. Appena sei positivo c’è qualcuno che ti chiama e ti chiede: “Quante persone hai visto? E chi sono?”. E poi si chiamano, si isolano e si seguono anche quelli». In pratica quello che stanno facendo in Cina, Corea e Hong Kong e in Europa la Germania. Vespignani poi spiega che non è necessario che l’isolamento duri 15 giorni per tutti ma va calcolato tenendo conto dei giorni che sono passati dal contatto con la persona positiva: «Siccome non va dimenticato che tutto questo ha un costo sociale enorme, se il contatto è avvenuto dieci giorni fa e sei negativo devi essere isolato solo cinque giorni»".
Il problema degli errori decisionali non è semplicemente l'ottusità degli esseri umani, ma il fenomeno di una "società non alfabetizzata al rischio"
Decessi Covid-19
Andamento dei decessi con e senza misure di contenimento
Infezioni Covid-19 a New York
Cliccare per approfondire
La matematica dell'incertezza che pochi studiano
Di solito si intende per statistica solo la cosiddetta "statistica descrittiva", che prende atto di ciò che accade e lo trasforma in numeri sulla base di rilevazioni effettuate sulla "popolazione" oggetto dell'indagine (ad esempio le statistiche ISTAT sull'intera popolazione).
Ma esiste un altro tipo di statistica, detta "statistica inferenziale", che prende un sottoinsieme limitato di misure (un "campione") e fa delle inferenze "rischiose" generalizzando all'intera popolazione le conclusioni probabilistiche svolte sul campione (ved. manipolazioni statistiche o manipolazione sondaggi elettorali).
Saper leggere e scrivere non è più sufficiente in una società tecnologica, sempre più complessa, nella quale i rischi si moltiplicano. Nè, tantomeno, è sufficiente saper far di conto in modo tradizionale, almeno questo è il parere dello psicologo Gerd Gigerenzer il quale sostiene che oggi, a scuola, si insegna ancora la "matematica della certezza" (geometria, trigonometria, ecc) ma non la "matematica dell'incertezza", cioè la "statistica inferenziale".
Per vivere nel mondo attuale occorrerebbe, secondo Gigerenzer, che la "buona scuola" insegnasse due competenze: una conoscenza di base della psicologia intuitiva e la capacità di capire le statistiche. Scrive Gigerenzer nel libro "Imparare a rischiare" (pp. 289-291):
Nelle situazioni quotidiane sono frequenti le occasioni in cui occorre calcolare delle probabilità (ad esempio, banalmente, qual è la probabilità di essere colpiti da un oggetto - tegola, albero, ecc - in una giornata di vento). Si tratta di calcolare la probabilità di un "evento singolo" alla luce di una condizione particolare, e questo è proprio il genere di compiti non risolvibili dall'essere umano secondo gli evoluzionisti (ved. bibliografia Girotto p.4).
Bisogna insegnare prima quello che è importante per la vita reale, e solo dopo quello che è importante in matematica. L'orientamento alla soluzione di problemi della vita reale anzichè a una matematica astratta rende essenziali una presentazione trasparente, strumenti pratici e regole del pollice intelligenti - ma per realizzare cose così nuove bisogna insegnare agli insegnanti.
Bisogna insegnare prima quello che è importante per la vita reale, e solo dopo quello che è importante in matematica. L'orientamento alla soluzione di problemi della vita reale anzichè a una matematica astratta rende essenziali una presentazione trasparente, strumenti pratici e regole del pollice intelligenti - ma per realizzare cose così nuove bisogna insegnare agli insegnanti.
Gli psicologi evoluzionisti (ved. bibliografia Cosmides e Tooby) sostengono invece che l'uomo si è evoluto per ragionare con le "frequenze di osservazione", cioè dopo avere osservato un certo numero di casi, è possibile inferire la probabilità che si verifichi una certa condizione (ad esempio, per una tribù di cacciatori-raccoglitori del Paleolitico: "nelle ultime 20 volte che siamo andati a caccia nelle montagne opposte al sole abbiamo catturato la preda 5 volte").
Ai nostri figli vengono insegnati l'algebra, la geometria, i fondamenti del calcolo infinitesimale e il calcolo infinitesimale stesso. In altre parole insegniamo loro la matematica della certezza e non quella dell'incertezza, ovvero il pensiero statistico
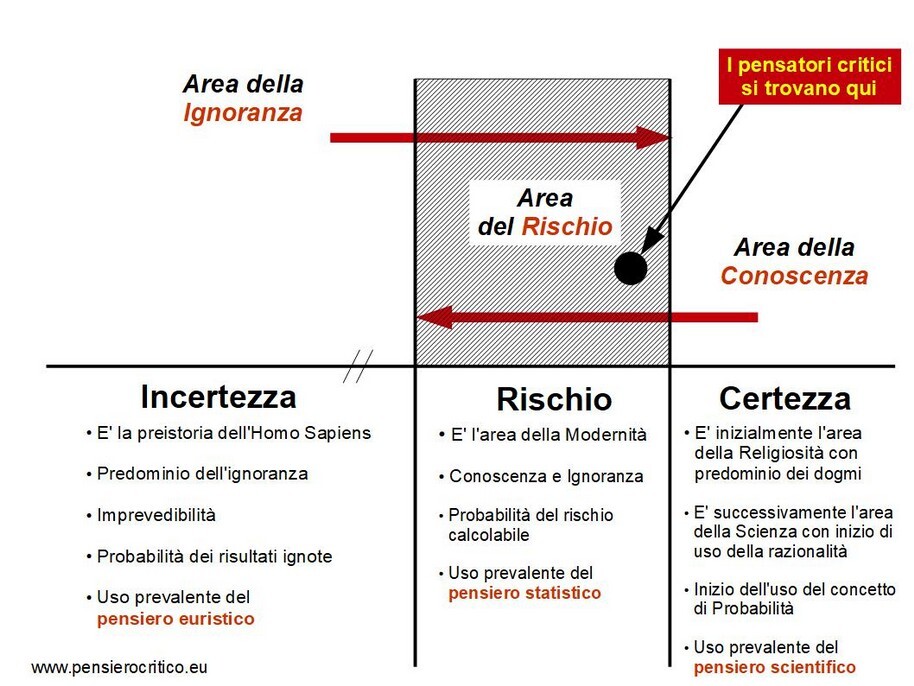
Tre aree per le azioni umane: certezza, incertezza e rischio
L'area "naturale" in cui si muove l'essere umano è quella dell'incertezza, enorme rispetto a quella della certezza (il disegno non mostra le reali proporzioni). Per affrontare il rischio, nell'antichità, l'uomo si affidava agli oracoli e ai suoi sacerdoti, ma solo dal secolo scorso ha imparato a calcolarlo.
La rivoluzione concettuale di Bayes e la probabilità "soggettiva"
La probabilità è un concetto antichissimo che risale alla modalità di pensiero evolutasi nel Paleolitico nella mente dei cacciatori-raccoglitori, i quali avevano una visione che oggi viene chiamata "frequentista", cioè come di una caratteristica intrinseca e "oggettiva" di un dato evento. La probabilità di un evento è così definita: "il rapporto fra il numero di esperimenti in cui esso si è verificato e il numero totale di esperimenti eseguiti nelle stesse condizioni, essendo tale numero opportunamente grande". Questa visione "oggettiva" della probabilità subisce una profonda modificazione a metà del 1700, con il Teorema del pastore presbiteriano Thomas Bayes, il quale inaugura una visione "soggettiva" della probabilità che la vede dipendere dall'esperienza accumulata dallo sperimentatore e, quindi, dal variare della sua conoscenza o ignoranza dell'evento.
Il Teorema di Bayes spiega come cambia la probabilità di un evento se (o dato che) sono accaduti altri eventi, quindi il Teorema di Bayes mostra come fare valutazioni di probabilità e modificarle successivamente in presenza di nuovi dati. Si parla quindi di "probabilità condizionata", le stime iniziali vengono dette "probabilità a priori" mentre le successive sono le "probabilità a posteriori". Nella "visione di Bayes" viene assegnata una probabilità a un'ipotesi (è il grado di fiducia che lo sperimentatore assegna) prima che essa venga verificata, mentre nella "visione frequentista" si può attribuire una probabilità a un'ipotesi solo dopo averne verificato gli effetti ripetutamente (è il caso della modalità di pensiero della citata tribù di cacciatori-raccoglitori), come mostrato nel seguente diagramma:
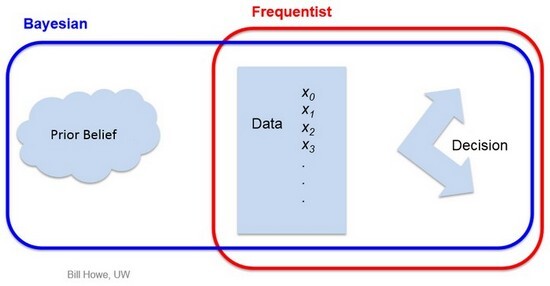
Appare quindi chiara l'importanza del Teorema di Bayes che, negli ultimi 30-40 anni, ha prodotto una rivoluzione concettuale nel pensiero umano consentendo lo sviluppo di molte nuove applicazioni tecnologiche (ad esempio: filtri antiSPAM, machine learning, intelligenza artificiale, ecc).
Il Teorema di Bayes ha introdotto una rivoluzione concettuale nel pensiero statistico, infatti riguardo a una complessa situazione specifica noi abbiamo sempre dei pre-giudizi (le informazioni iniziali) che permettono di assegnare all'evento una prima probabilità (probabilità a priori). Successivamente, però, il pensatore critico può mettere in funzione il suo "motore inferenziale" e, applicando la formula di Bayes, può calcolare la probabilità a posteriori, sulla base di specifici indizi, cioè la probabilità "condizionata" da quegli indizi.
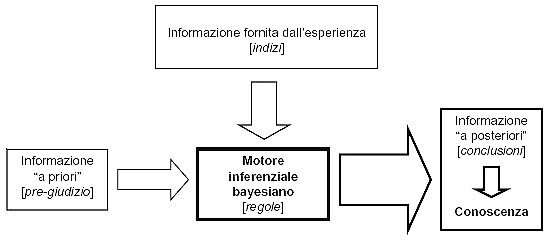
Il motore inferenziale e la probabilità "condizionata"
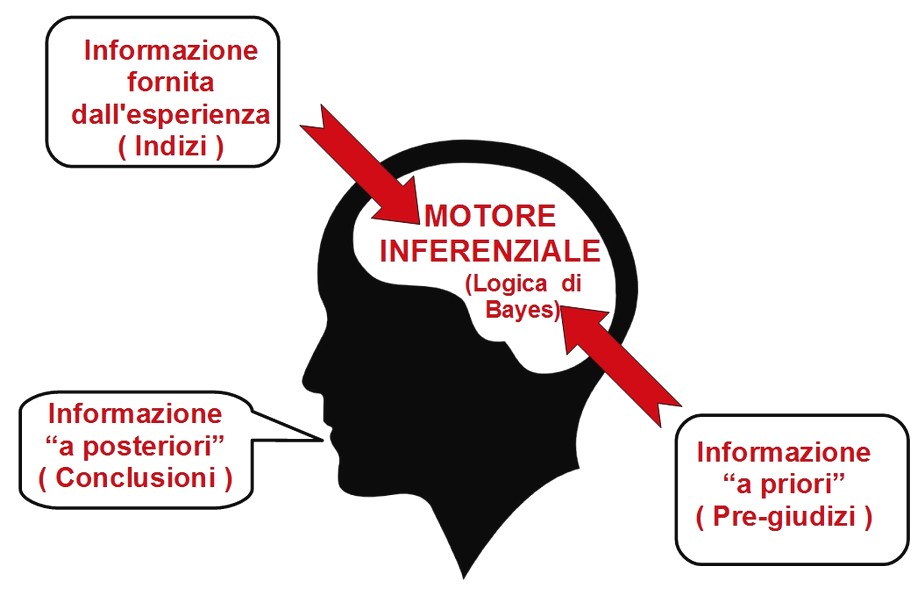
La logica di Bayes è un termine improprio che indica l'applicazione del Teorema di Bayes a una situazione specifica nella quale l'individuo si trova ad avere alcune informazioni iniziali (pre-giudizi) che gli permettono di assegnare all'evento una prima probabilità (probabilità a priori). Successivamente egli può mettere in funzione il suo "motore inferenziale" e, applicando la formula di Bayes, può calcolare la probabilità a posteriori, sulla base di specifici indizi, cioè la probabilità "condizionata" da quegli indizi.
Ponendo che A sia l'ipotesi e B sia l'evidenza che la conferma, il Teorema di Bayes è espresso dalla formula che segue.
Formula di Bayes
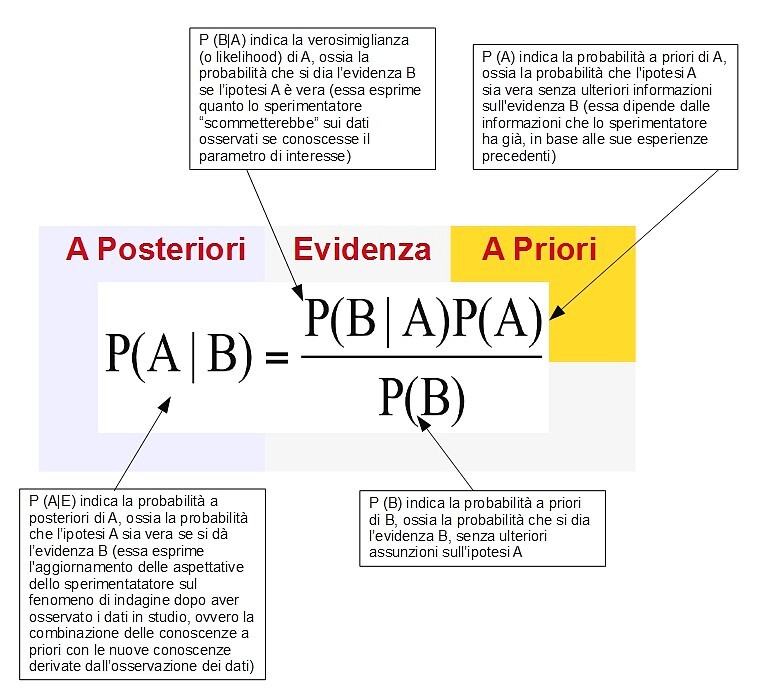
lI Teorema di Bayes mostra come fare valutazioni di probabilità e modificarle successivamente in presenza di nuovi dati. Si parla quindi di "probabilità condizionata", le stime iniziali vengono dette "probabilità a priori" mentre le successive sono le "probabilità a posteriori"
Decisioni medico-diagnostiche
Il teorema di Bayes è molto impiegato in medicina nelle valutazioni diagnostiche dato che esso, attraverso i risultati della sua formula mostra come le credenze esistenti, formalmente espresse come distribuzioni di probabilità, possano essere modificate da nuove informazioni. I test diagnostici costituiscono una di quelle situazioni alle quali il teorema può essere applicato migliorando la prima convinzione del medico sulla presenza di una particolare malattia in un suo paziente (basata sia sui sintomi del paziente sia sulla conoscenza della prevalenza della malattia in quella comunità), e modificandone il giudizio in funzione del risultato del test.
I test non sempre sono veritieri, cioè aderenti alla realtà. Vi sono cose che non esistono ("falsi positivi") e mancano cose che esistono ("falsi negativi"). Risultare positivi a un test HIV o a un test tumorale è cosa diversa da avere effettivamente la sindrome da immunodeficienza acquisita o il tumore, infatti i test vanno ripetuti per eliminare i falsi positivi. Eppure spesso le persone, anche i medici, considerano i risultati dei test come se fossero esenti da errori.
Un ottimo sito per migliorare le decisioni mediche con l'approccio bayesiano è quello di Marco Besozzi che offre ai medici, anche fogli di calcolo e altri strumenti per esercitarsi. Besozzi mette a confronto i tre approcci della statistica (classica, frequentista, bayesiana con interpretazione soggettiva) e ne evidenzia l'applicabilità o meno alle decisioni diagnostiche, in cui mette in rilievo l'importanza della relazione di verosimiglianza.
Il sito Bayes.it offre molte pagine che descrivono nel dettaglio i concetti statistici tra le quali, per coloro che volessero approfondire, consiglio le seguenti:
Esempio applicativo
La formula di Bayes utile alle decisioni diagnostiche è la seguente:
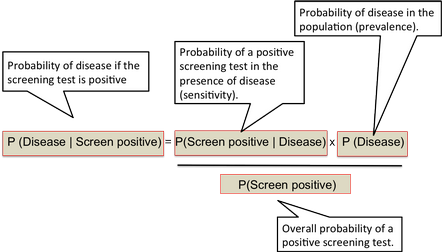
Questa rappresentazione evidenzia le varie probabilità coinvolte nello screening di una malattia. Un caso con maggiori indizi è quello citato dallo psicologo Vittorio Girotto in ("Gli errori del ragionamento" ved. bibliografia pp. 4-5):
- Una persona sottoposta al test ha il 4% di probabilità di aver contratto la malattia.
- Se una persona ha contratto la malattia, ha il 75% di probabilità di avere una reazione positiva al test.
Definendo H l’ipotesi “Paolo malato”, -H l’ipotesi “Paolo sano”, e D il dato “Paolo positivo”, allora p(H|D), cioè la probabilità condizionata (probabilità a posteriori) che Paolo sia malato se è positivo, sarà:p(H|D) = p(D|H) x p(H) / [p(D|H) x p(H) + p(D|non-H) x p(non-H)] = (75% x 4%) / [75% x 4% + 12,5% x (100% - 4%)] = 3% / (3% + 12%) = 20%
Buone rappresentazioni aiutano la comprensione
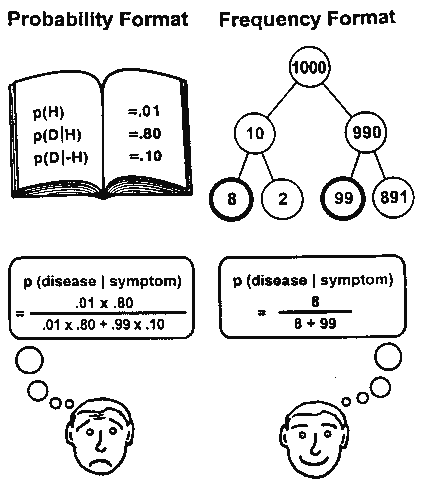
Gli psicologi Ulrich Hoffrage, Gerd Gigerenzer et Al. (ved. bibliografia 2002), hanno evidenziato l'importanza delle rappresentazioni grafiche dei problemi per favorire la comprensione e arrivare rapidamente alla soluzione. Nell'immagine soprastante viene mostrata la semplificazione della rappresentazione trasformando la formula di Bayes in frequenze naturali, cioè costruendo un albero che divida i malati (10) dai non malati (990) e, successivamente, per ognuna delle due categorie coloro che risultano positivi al test (8+99).
Le buone rappresentazioni grafiche dei problemi sono importanti per favorire la comprensione e arrivare rapidamente alla soluzione del problema
La curva di Gauss che separa i cigni bianchi da quelli neri
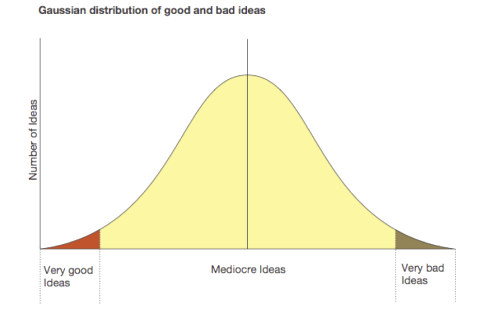
Differenza tra il mondo stabile e prevedibile delle "medie" e il mondo (a volte) instabile e imprevedibile della realtà
Lo statistico Nassim Taleb ha fatto dell'avversione per la distribuzione gaussiana, diventata un simbolo statistico, l'oggetto principale della sua avversione che egli descrive dettagliatamente nel suo libro più famoso ("Il cigno nero" pp. 242-264). Secondo Taleb, nella teoria statistica, l'incertezza insita nella vita svanisce nelle medie che la curva gaussiana rappresenta (cioè in quello che egli chiama "Mediocristan"). Per la legge dei grandi numeri il concetto di "deviazione standard" non esiste al di fuori della gaussiana, alimentando il riduzionismo degli illusi che si nutrono di "medie". Taleb sostiene che la curva a campana di Gauss non è onnipresente nella realtà ma esiste solo nella mente degli statistici e nasce dal modo con cui essi guardano al mondo. Per questo egli distingue tra il mondo "prevedibile" che le gaussiane rappresentano (il "Mediocristan") e il mondo reale incerto e imprevedibile (l' "Estremistan). Egli scrive (pp.250, 257):
[Nel Mediocristan] nessuna osservazione singola può avere un impatto sul totale. Questa proprietà diventa sempre più significativa via via che la popolazione aumenta di dimensioni. Le medie diventeranno sempre più stabili, al punto che tutti i campioni si assomiglieranno. [E invece, nell'Estremistan] un singolo numero può sovvertire tutte le medie calcolate; una singola perdita può annientare un secolo di guadagni. "Be', posso perdere soldi" non è un'informazione, a meno che non si quantifichi la perdita. Si può perdere tutto il proprio patrimonio oppure soltanto una frazione del proprio reddito quotidiano: c'è una bella differenza.
The average life expectancy continues to lenghten.
Someone inform it that there is no more meat on the bone.
Someone inform it that there is no more meat on the bone.
Secondo Nassim Taleb, nella teoria statistica, l'incertezza insita nella vita svanisce nelle medie che la curva gaussiana rappresenta (cioè in quello che egli chiama "Mediocristan"). Per la legge dei grandi numeri il concetto di "deviazione standard" non esiste al di fuori della gaussiana, alimentando il riduzionismo degli illusi che si nutrono di "medie". Taleb sostiene che la curva a campana di Gauss non è onnipresente nella realtà ma esiste solo nella mente degli statistici e nasce dal modo con cui essi guardano al mondo
Esempio1: probabilità di un tradimento
Il fisico Leonard Mlodinow cita nel suo libro "La passeggiata dell'ubriaco", molti esempi di applicazione del Teorema di Bayes alla vita quotidiana, tra i quali il seguente (pp. 126-127):
Infatti la probabilità che "la tradisse se andava in giro di nascosto" è molto più bassa della probabilità che "andasse in giro di nascosto se la tradiva", perchè il marito poteva avere molte altre buone ragioni (e il film ne mostra solo una) per andare in giro di nascosto. La differenza tra le due opzioni sembra piccola ma non lo è: provate a rifletterci un po'...
Esempio2: i filtri antiSPAM
La maggior parte dei filtri antiSPAM odierni usano l'approccio Bayesiano per la sua efficacia. Esso si basa su un database iniziale contenente sia messaggi spam sia messaggi non spam. Il database iniziale viene utilizzato per l'apprendimento del filtro anti-spam, che avviene conteggiando, per ogni parola che compare in quei messaggi, il numero di volte che essa appare nei messaggi spam e in quelli non-spam. Questo conteggio aiuta a stimare quante volte quella parola compare in spam e non spam e a calcolare la probabilità corrispondente. Il risultato che il filtro ottiene sono due elenchi (spam e non-spam) di parole usate e le probabilità corrispondenti. Le liste vengono utilizzate per stimare la probabilità che un nuovo messaggio sia spam. Quando si riceve un nuovo messaggio l'algoritmo del filtro anti-spam lo suddivide in parole e le cerca in entrambe le liste. Usando le probabilità per le singole parole delle due liste e applicando la formula di Bayes il programma stima la probabilità che l'intero messaggio sia spam o non-spam.
L'efficacia del filtraggio spam dipende dal contenuto del database usato per l'apprendimento del filtro. Quindi, per rendere il filtraggio più efficace per uno specifico utente è necessario che il filtro impari dal database messaggi di quell'utente e aggiusti automaticamente il filtraggio in base alle retroazioni dell'utente.
Esempio3: probabilità di un complotto
Perchè le teorie del complotto sono molto diffuse sia nelle nostre menti, sia in quelle dei giornalisti o dei politici? La teoria di un complotto contro di sè o contro un gruppo sociale è radicata nella mente di molti di noi e viene spesso sfruttata "ad arte" dai media. Tale teoria sfrutta l'incapacità di fare inferenze statistiche insieme a una tendenza paranoide, ed è un errore che facciamo spesso nella vita quotidiana come ha scritto Leonard Mlodinow nel suo libro "La passeggiata dell'ubriaco", egli scrive (pp. 128):
Come Bayes aiuta a pensare in modo nuovo ma...senza esagerare
Negli ultimi anni l'importanza del Teorema di Bayes è stata abusata attribuendo alla formula un potere "quasi magico", e vi sono psicologi come Matt Jones e Bradley C. Love (ved. bibliografia) che parlano addirittura di "fondamentalismo bayesiano". Se si vuol dare il giusto valore al Teorema si può dire che esso è uno dei modi migliori per riflettere sulle "evidenze", e per mettere in discussione i propri pregiudizi sul mondo, e per "tentare" di contrastare i bias cognitivi (e in particolare il confirmation bias). Secondo il giornalista scientifico John Horgan (ved. bibliografia 2016), il lascito morale del Teorema di Bayes è il seguente:
Quindi si può dire che la formula di Bayes è una formalizzazione statistica di come cambiare idea quando si apprendono nuove informazioni sul mondo o si fanno nuove esperienze. Occorre accettare il fatto che le proprie convinzioni su come funziona il mondo non sono assolute, e che quando si va per il mondo e si incontrano nuove idee e nuove evidenze, il proprio livello di fiducia deve "fluttuare" via via che si incontrano prove a favore o contro le proprie convinzioni, ed è meglio che sia così.
In fondo applicare Bayes equivale a una iniezione di umiltà per contrastare le rigidità del proprio pensiero.
Nel video a fianco vengono mostrate alcune applicazioni , del teorema di Bayes alla vita quotidiana, di Julia Galef, scettica e statistica.
Come il pensiero bayesiano può aiutare a pensare razionalmente nella vita quotidiana
Video in inglese - abilitare i sottotitoli
The reason turned out to be a speculative bubble
La formula di Bayes è una formalizzazione statistica di come cambiare idea quando si apprendono nuove informazioni sul mondo o si fanno nuove esperienze
La razionalità richiede impegno personale!
Iscriviti alla Newsletter di pensierocritico.eu per ricevere in anteprima nuovi contenuti e aggiornamenti:
Iscriviti alla Newsletter di pensierocritico.eu per ricevere in anteprima nuovi contenuti e aggiornamenti:
Bibliografia (chi fa delle buone letture è meno manipolabile)
- Ruth Beyth-Maron, Fiona Fidler, Geoff Cumming (2008), STATISTICAL COGNITION: TOWARDS EVIDENCE-BASED PRACTICE IN STATISTICS AND STATISTICS EDUCATION (PDF) - Articolo che descrive le tendenze di ricerca accademica nella Statistica con molti riferimenti
- Jean-Marie Robine (2008), Tra compressione e declino della mortalità: la rivoluzione della longevità
- Ezio Bottarelli (2015), Variabilità biologica, deviazione standard e normalità
- Joel B. Greenhouse (2013), Statistical Thinking: The Bedrock of Data Science
- C.J. Wild and M. Pfannkuch (1999), Statistical Thinking in Empirical Enquiry (PDF) [904 citazioni]
- (2015), Risks and Statistics
- Frank H. Knight (1911), Risk, Uncertainty, and Profit - L'intero libro è consultabile online
- Giuseppe Carichino, Probabilità condizionata e teorema di Bayes - YouMath
- Gianfranco Bo, Introduzione alla regola di Bayes
- Marco Besozzi (2013), Errori cognitivi, probabilità e decisione mediche - Applicazioni e utilità del teorema di Bayes nella diagnostica di laboratorio (PDF) - eBook che ricostruisce la storia delle idee filosofiche della razionalità umana applicandole alle strategie diagnostiche
- Defining and Distinguishing Statistical Literacy, Statistical Reasoning, and Statistical Thinking
- Gianfranco Bo (2014), Introduzione alla regola di Bayes - Esercizi ed esempi
- Geoffrey T. Fong et Al. (1986), The Effects of Statistical Training on Thinking about Everyday Problems (PDF)
- Jane M. Watson (1997), Assessing Statistical Thinking Using the Media (PDF)
- Vittorio Girotto (2005), Gli errori nel ragionamento (PDF)
- Leda Cosmides, John Tooby (1996), Are humans good intuitive statisticians after all? Rethinking some conclusions from the literature on judgment under uncertainty (PDF)
- F. D. Flam (2014), The Odds, Continually Updated - The New York Times
- Richard Carrier (2012), Bayesian Calculator - Strumento per calcolare rapidamente online la probabilità di un evento date certe condizioni (impostabili)
- John Horgan (2016), Bayes's Theorem: What's the Big Deal? - Scientific American - Articolo critico sull'estensibilità del Teorema di Bayes a tutti i campi scientifici
- Matt Jones, Bradley C. Love (2011), Bayesian Fundamentalismor Enlightenment? On the explanatorystatus and theoretical contributions of
- Statistical Literacy - Sito dedicato alla cultura statistica con molti articoli e riferimenti
- Ulrich Hoffrage, Gerd Gigerenzer, Stefan Krauss, Laura Martignon (2002),Representation facilitates reasoning: what natural frequencies are and what they are not (PDF)
- Brandon Rohrer (2016), How Bayesian inference works
- Luca Tremolada (2011), Campione inconscio - Sole24Ore
- Gabriella Canova (2020), L’epidemiologo Vespignani spiega come agire contro il covid-19 - People for Planet
Scrivi, se non sei d'accordo
Se ritenete che le tesi del "punto chiave" non vengano sufficientemente supportate dagli argomenti presenti in questa pagina potete esprimere il vostro parere (motivandolo).
Inviate una email con il FORM. Riceverete una risposta. Grazie della collaborazione.
Guarda le pagine correlate
Libri consigliati
a chi vuole capire il pensiero statistico
a chi vuole capire il pensiero statistico
Spesa annua pro capite in Italia per gioco d'azzardo 1.583 euro, per l'acquisto di libri 58,8 euro (fonte: l'Espresso 5/2/17)
Pagina aggiornata il 25 agosto 2023